Vectors¶
variationalform https://variationalform.github.io/¶
Just Enough: progress at pace¶
https://variationalform.github.io/
https://github.com/variationalform
Simon Shaw https://www.brunel.ac.uk/people/simon-shaw.
|
|
This work is licensed under CC BY-SA 4.0 (Attribution-ShareAlike 4.0 International) Visit http://creativecommons.org/licenses/by-sa/4.0/ to see the terms. |
| This document uses python |

|
and also makes use of LaTeX |

|
in Markdown |
|
What this is about:¶
You will be introduced to ...
- Vectors as a way to think about points in space.
- The arithmetic (adding and subtracting) of vectors.
- Ways to measure the size - or length - of a vector.
- The
numpylibrary (or package) for working with vectors inpython.
We'll then see how to interpret data as vectors in high dimensional space. This will involve abstraction in that although it's easy for us to visualize a point in three dimensions, data may live in many dimensions.
As usual our emphasis will be on doing rather than proving: just enough: progress at pace.
Assigned Reading¶
For this worksheet you should read sections 1.1 - 1.3 and 3.1, 3.2 of [VMLS] for background
to the linear algebra of vectors, and also Appendix D of [DSML] if you want to read more
about python and numpy.
- VMLS: Introduction to Applied Linear Algebra - Vectors, Matrices, and Least Squares, by Stephen Boyd and Lieven Vandenberghe, https://web.stanford.edu/~boyd/vmls/
- DSML: Data Science and Machine Learning, Mathematical and Statistical Methods by Dirk P. Kroese, Zdravko I. Botev, Thomas Taimre, Radislav Vaisman, https://people.smp.uq.edu.au/DirkKroese/DSML and https://people.smp.uq.edu.au/DirkKroese/DSML/DSML.pdf
Further accessible material can be found in [FCLA], and the early part of Chapter 1 of [SVMS]. Advanced material is available in Chapters 2 and 3 of [MML].
- MML: Mathematics for Machine Learning, by Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong. Cambridge University Press. https://mml-book.github.io.
- FCLA: A First Course in Linear Algebra, by Ken Kuttler, https://math.libretexts.org/Bookshelves/Linear_Algebra/A_First_Course_in_Linear_Algebra_(Kuttler)
- SVMS: Support Vector Machines Succinctly, by Alexandre Kowalczyk, https://www.syncfusion.com/succinctly-free-ebooks/support-vector-machines-succinctly
- VMLS: Introduction to Applied Linear Algebra - Vectors, Matrices, and Least Squares, by Stephen Boyd and Lieven Vandenberghe, https://web.stanford.edu/~boyd/vmls/
All of the above can be accessed legally and without cost.
There are also these useful references for coding:
- PT:
python: https://docs.python.org/3/tutorial - NP:
numpy: https://numpy.org/doc/stable/user/quickstart.html - MPL:
matplotlib: https://matplotlib.org
Vectors¶
A vector is a row or column of real numbers enclosed in brackets. For example, these
$$ \boldsymbol{v} = (3, -2, 1),\qquad \boldsymbol{b} = \left(\begin{array}{r} 6 \\ -3 \\ 2.5 \\ -1 \\ 0 \end{array}\right) $$show a row vector in $\mathbb{R}^3$, and a column vector in $\mathbb{R}^5$, where $\mathbb{R}^n$ denotes the $n$-dimensional set of real numbers (to get feel for this we live in $\mathbb{R}^3$ - up/down, forward/backward and left/right). We will denote vectors by lower case bold letters. A vector $\boldsymbol{v}$ in $\mathbb{R}^n$, written as $\mathbb{v} \in \mathbb{R}^n$ is said to have dimension $n$.
Note that we use commas to make it clear that the numbers are separate entities, but the commas are not part of the vector. We often think of vectors as having physical meaning, and then we diagrammatically represent them with arrows.
For example, the diagram here https://en.wikipedia.org/wiki/Euclidean_vector#/media/File:Position_vector.svg, taken from https://en.wikipedia.org/wiki/Euclidean_vector, shows a row vector in $2$ dimensions, joining the origin at $O$ to the coordinate $(x,y)=(2,3)$ at $A$.
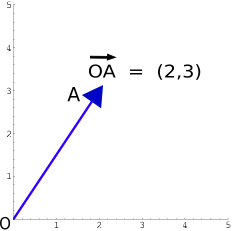
This vector has components of length $2$ in the $x$ direction and of length $3$ in the $y$ direction. The overall length of the vector is then $\sqrt{2^2+3^2} = \sqrt{13}\approx 3.605$ by Pythagoras's theorem. This might for example represent a person cycling approximately north-east at $3.6\,\mathrm{km/h}$ - or $2\,\mathrm{km/h}$ east and, simultaneously, $3\,\mathrm{km/h}$ north.

Note that the coordinate $(2,3)$ at $A$ in the diagram could easily be confused with a row vector. Such overloading of notation is common in maths, and usually context makes it clear what is intended.
This shouldn't happen for us though, because from now on we will always work with column vectors, and switch between column and row forms using the the transpose operation. The transpose of a vector is denoted with a superscript $T$ and swaps the row into a column and vice-versa. For example,
$$ \boldsymbol{v}^T = \left(\begin{array}{r}3 \\ -2 \\ 1\end{array}\right), \qquad \boldsymbol{b}^T = (6, -3, 2.5, -1, 0). $$python: Binder, Anaconda and Jupyter¶
We will use binder, and then the anaconda distribution to access python and the libraries we need. The
coding itself will be carried out in Jupyter notebooks. We'll go through this in an
early lab session so you can get started with 'hands on' machine learning.
Using numpy to represent vectors¶
The numpy module (or library) is the main tool for scientific computing
in python. It stands for numerical python, and it will be a key tool
for us. See https://numpy.org
We load in the numpy package and abbreviate it with np as follows.
This syntax is very standard. You can use something other than np
if you like, but you'll be swimming against the tide.
import numpy as np
Now we can set up two vectors as numpy arrays, and print them out, as follows,
v = np.array([3,-2,1])
b = np.array([ [6], [-3], [2.5], [-1], [0]])
print('v = ', v, ' and b = ', b)
v = [ 3 -2 1] and b = [[ 6. ] [-3. ] [ 2.5] [-1. ] [ 0. ]]
This looks a bit messy - let's try again, forcing a line break
print(v, '\n', b)
[ 3 -2 1] [[ 6. ] [-3. ] [ 2.5] [-1. ] [ 0. ]]
This is a bit better - you can see how numpy handles row and column vectors.
We'll often not worry about the distinction between row and column vectors
when using numpy. It's easier (i.e. less typing) to set up the row
vector above, and we'll often take that route. Although when we write
vectors mathematically we will always use column vectors.
Using numpy for transpose.¶
We can write b.T for $\boldsymbol{b}^T$, but the overall effect is is a bit unexpected.
print('v = ', v.T, ' and b = ', b.T)
v = [ 3 -2 1] and b = [[ 6. -3. 2.5 -1. 0. ]]
It's a bit hard to see what is going on - the key thing to remember is that these objects are arrays in computer memory, and not mathematical vectors.
You can get the behaviour you expect with this.
v = np.array([[3,-2,1]])
print(v.T)
[[ 3] [-2] [ 1]]
Alternatively, you can force the shape by using the shape attribute - take a look
at these... (note that # is used to write comments)
# this gives a list of numbers.
a = np.array([3, -2, 1])
print(a)
# ask for the shape - it is just (3,)
a.shape
# force the shape to be 3-row by 1-column
a.shape = (3,1)
print(a)
# now print the transpose
print(a.T)
[ 3 -2 1] [[ 3] [-2] [ 1]] [[ 3 -2 1]]
Here is a different approach...
# force b to have one row - a row vector
b = np.array([[3, -2, 1]])
print(b)
print('The shape of b is ', b.shape)
# and then transpose it to get a column vector
b = np.array([[3, -2, 1]]).T
print(b)
[[ 3 -2 1]] The shape of b is (1, 3) [[ 3] [-2] [ 1]]
For a bit more discussion see e.g. https://stackoverflow.com/questions/17428621/python-differentiating-between-row-and-column-vectors
We wont have to worry too much about these subtle things - the python libraries that we will use will take care of all of this bookkeeping.
Addition and Subtraction¶
Vectors of the same shape can be added or subtracted, component by component. For example, forming $\boldsymbol{g}=\boldsymbol{a}-\boldsymbol{p}$ with
$$ \boldsymbol{a} = \left(\begin{array}{r} 3\\ -2\\ 1 \end{array}\right) \text{ and } \boldsymbol{p} = \left(\begin{array}{r} 5\\ 2\\ -10 \end{array}\right) \text{ then gives } \boldsymbol{g} = \left(\begin{array}{r} 3-5\\ -2-2\\ 1-(-10) \end{array}\right) = \left(\begin{array}{r} -2\\ -4\\ 11 \end{array}\right). $$You can check that $\boldsymbol{a}=\boldsymbol{g}+\boldsymbol{p}$, as we would expect.
A visual demonstration of this addtion process can be accessed here: https://www.geogebra.org/m/hm4haajh in two dimensions, and here https://www.geogebra.org/m/drvu2f66 in three dimensions. The idea is similar in higher dimensions but harder to draw.
Vector - scalar multiplication¶
A vector can be multiplied by a scalar just by multiplying each element of the vector by that same scalar. For example:
$$ \text{if }\qquad \boldsymbol{y} = \left(\begin{array}{r} -3 \\ 16 \\ 1 \\ 1089 \\ 15 \end{array}\right) \qquad\text{ then }\qquad \boldsymbol{-3y} = \left(\begin{array}{r} 9 \\ -48 \\ -3 \\ -3267 \\ -45 \end{array}\right) $$Using numpy for vector calculations¶
We'll set up the vectors $\boldsymbol{a}$ and $\boldsymbol{p}$ given above
as numpy arrays and then show how to do these operations in python.
a = np.array([3, -2, 1])
p = np.array([5, 2, -10])
g = a-p
print(g)
a = g+p
print(a)
[-2 -4 11] [ 3 -2 1]
y = np.array([-3, 16, 1, 1089, 15])
z = -3*y
print(z)
[ 9 -48 -3 -3267 -45]
Vector Norms¶
In mathematics the word norm is used to denote the size of something. Depending on what that 'something' is, its 'size' can be an 'obvious' property, or much more abstract. The most obvious way to measure the size of a vector is to use its length. We'll start by examining that, and then move on to more general notions.
The Vector $2$-norm ($\ell_2$, or Euclidean, or Pythagorean, distance)¶
In general, for a vector $\boldsymbol{v}\in\mathbb{R}^n$ (a point beloging to $n$-dimensional space), with $n$ components $v_1$, $v_2$, $\ldots$, $v_n$, we denote its Pythagorean (or Euclidean) length by the so-called $2$-norm:
$$ \Vert\boldsymbol{v}\Vert_2 = \sqrt{v_1^2 + v_2^2 +\cdots+v_n^2}. $$If you visualize the $2$-norm you will probably think of the 'as the crow flies' distance between any two points $A$ and $B$.
Example:¶
Suppose we have this vector
$$ \boldsymbol{u} = \left(\begin{array}{r} -3 \\ 2 \\ 4 \\ -1 \end{array}\right) $$Then,
$$ \Vert\boldsymbol{u}\Vert_2 = \sqrt{(-3)^2 + 2^2 + 4^2 + (-1)^2 } = \sqrt{9+4+16+1} = \sqrt{30} \approx 5.477\ldots $$Let's see how to do this with numpy. We'll use the linear algebra
submodule, https://numpy.org/doc/stable/reference/routines.linalg.html,
and the norm function,
https://numpy.org/doc/stable/reference/generated/numpy.linalg.norm.html.
u = np.array([-3, 2, 4, -1])
print('||u||_2 = ', np.linalg.norm(u))
# We can also specify the '2'
print('||u||_2 = ', np.linalg.norm(u, 2))
||u||_2 = 5.477225575051661 ||u||_2 = 5.477225575051661
The Vector $p$-norm ($\ell_p$, or Minkowski, norms)¶
Being able to specify the power/root of $2$ is useful because there are other norms corresponding to other values of the power and root.
More generally, we can use the $p$-norm for any $p\ge 1$ where
$$ \Vert\boldsymbol{v}\Vert_p = \left\{\begin{array}{ll}\displaystyle \sqrt[p]{\vert v_1\vert^p + \vert v_2\vert^p +\cdots+\vert v_n\vert^p}, &\text{if } 1\le p < \infty; \\ \max\{\vert v_k\vert\colon k=1,2,\ldots,n\}, &\text{if } p = \infty. \end{array}\right. $$These norms will be very useful to us in the applications we study later. Often the $p$-norm will also be referred to as the $\ell_p$ norm.
Note that $p<1$ is not allowed in this definition. That doesn't, however, stop some casual usage whereby the definition above is extended to $p<1$ to get $\ell_p$ norms for $p<1$. This means that quantities like an $\ell_{1/2}$, given by $\Vert\boldsymbol{v}\Vert_{1/2}$, get used as 'norms'.
Strictly speaking these aren't norms when $p<1$ (see {Chap. 3, MML} https://mml-book.github.io), although in practice these quantities can be useful. We could call them phoney norms.
An extreme example is the $\ell_0$ norm. This gives the number of non-zero elements in a vector. It is not a norm, but is nevertheless useful when sparsity is of interest.
Apart from the Euclidean/Pythagorean $2$-norm that we saw above, the $1$-norm and the $\infty$-norms are also of importance.
The Vector $1$-norm ($\ell_1$, Manhattan, or taxicab, distance)¶
The $1$ norm is often referred to as the Manhattan distance because (in 2D) the we can get from point $A$ to point $B$ by only moving along coordinate directions. This can be an 'L-shape' or any number of staircase paths. See for example, https://en.wikipedia.org/wiki/Taxicab_geometry

This is akin to how one moves from one point to another in the street-grid system in Manhattan, either on foot or in a taxi.
The Vector $\infty$-norm ($\ell_\infty$, 'max', or Chebychev, norm)¶
This doesn't really measure the distance from $A$ to $B$ but instead just records the largest (in absolute value) length along the coordinate directions.
Example:¶
Suppose we have this vector
$$ \boldsymbol{w} = \left(\begin{array}{r} 3 \\ -2 \\ -4 \\ 1 \end{array}\right) $$Then,
$$ \Vert\boldsymbol{w}\Vert_\infty = \max\{\vert w_k\vert\colon k=1,2,3,4\} = 4 $$Example¶
Let's work some more examples by hand and then with numpy. Let,
Then
$$ \Vert\boldsymbol{w}\Vert_2 = \sqrt{361+324+4+0+0+64+1156+0+3249} = \sqrt{5158} \approx 71.819\ldots $$Also,
$$ \Vert\boldsymbol{w}\Vert_1 = 19+18+2+0+0+8+34+0+57 = 138, \qquad \Vert\boldsymbol{w}\Vert_\infty = 57 \qquad\text{ and }\qquad \Vert\boldsymbol{w}\Vert_0 = 6 $$Let's see these in numpy.
w = np.array([-19, 18, 2, 0, 0, -8, 34, 0, -57])
print('||w||_2 = ', np.linalg.norm(w,2))
print('||w||_1 = ', np.linalg.norm(w,1))
print('||w||_inf = ', np.linalg.norm(w,np.inf)) # note how we denote infinity
print('||w||_0 = ', np.linalg.norm(w,0))
||w||_2 = 71.8192174839019 ||w||_1 = 138.0 ||w||_inf = 57.0 ||w||_0 = 6.0
Some data - data as vectors¶
Let's now look at some data. Just as before, in the following cell we import seaborn and look at
the names of the built-in data sets. The seaborn library, https://seaborn.pydata.org,
is designed for data visualization. It uses matplotlib, https://matplotlib.org,
which is a graphics library for python.
More detail on the datasets can be found here: https://github.com/mwaskom/seaborn-data/blob/master/README.md
If you want to dig deeper, you can look at https://blog.enterprisedna.co/how-to-load-sample-datasets-in-python/ and https://github.com/mwaskom/seaborn-data for the background - but you don't need to.
The first part of the following material we have seen before. This is a recap.
import seaborn as sns
# we can now refer to the seaborn library functions using 'sns'
# note that you can use another character string - but 'sns' is standard.
# Now let's get the names of the built-in data sets.
sns.get_dataset_names()
# type SHIFT=RETURN to execute the highlighted (active) cell
['anagrams', 'anscombe', 'attention', 'brain_networks', 'car_crashes', 'diamonds', 'dots', 'dowjones', 'exercise', 'flights', 'fmri', 'geyser', 'glue', 'healthexp', 'iris', 'mpg', 'penguins', 'planets', 'seaice', 'taxis', 'tips', 'titanic', 'anagrams', 'anagrams', 'anscombe', 'anscombe', 'attention', 'attention', 'brain_networks', 'brain_networks', 'car_crashes', 'car_crashes', 'diamonds', 'diamonds', 'dots', 'dots', 'dowjones', 'dowjones', 'exercise', 'exercise', 'flights', 'flights', 'fmri', 'fmri', 'geyser', 'geyser', 'glue', 'glue', 'healthexp', 'healthexp', 'iris', 'iris', 'mpg', 'mpg', 'penguins', 'penguins', 'planets', 'planets', 'seaice', 'seaice', 'taxis', 'taxis', 'tips', 'tips', 'titanic', 'titanic', 'anagrams', 'anscombe', 'attention', 'brain_networks', 'car_crashes', 'diamonds', 'dots', 'dowjones', 'exercise', 'flights', 'fmri', 'geyser', 'glue', 'healthexp', 'iris', 'mpg', 'penguins', 'planets', 'seaice', 'taxis', 'tips', 'titanic']
The taxis data set¶
# let's take a look at 'taxis'
dft = sns.load_dataset('taxis')
# this just plots the first few lines of the data
dft.head()
| pickup | dropoff | passengers | distance | fare | tip | tolls | total | color | payment | pickup_zone | dropoff_zone | pickup_borough | dropoff_borough | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2019-03-23 20:21:09 | 2019-03-23 20:27:24 | 1 | 1.60 | 7.0 | 2.15 | 0.0 | 12.95 | yellow | credit card | Lenox Hill West | UN/Turtle Bay South | Manhattan | Manhattan |
| 1 | 2019-03-04 16:11:55 | 2019-03-04 16:19:00 | 1 | 0.79 | 5.0 | 0.00 | 0.0 | 9.30 | yellow | cash | Upper West Side South | Upper West Side South | Manhattan | Manhattan |
| 2 | 2019-03-27 17:53:01 | 2019-03-27 18:00:25 | 1 | 1.37 | 7.5 | 2.36 | 0.0 | 14.16 | yellow | credit card | Alphabet City | West Village | Manhattan | Manhattan |
| 3 | 2019-03-10 01:23:59 | 2019-03-10 01:49:51 | 1 | 7.70 | 27.0 | 6.15 | 0.0 | 36.95 | yellow | credit card | Hudson Sq | Yorkville West | Manhattan | Manhattan |
| 4 | 2019-03-30 13:27:42 | 2019-03-30 13:37:14 | 3 | 2.16 | 9.0 | 1.10 | 0.0 | 13.40 | yellow | credit card | Midtown East | Yorkville West | Manhattan | Manhattan |
Recall that what we are seeing here is a data frame.
It is furnished by the pandas
library: https://pandas.pydata.org which is used by the seaborn library
to store its example data sets.
In this, the variable dft is a pandas data frame: dft = data frame taxi
Each row of the data frame corresponds to a single data point, which we
could also call an observation or measurement (depending on context).
Each column (except the left-most) corresponds to a feature of the data point. The first column is just an index giving the row number. Note that this index starts at zero - so, for example, the third row will be labelled/indexed as $2$. Be careful of this - it can be confusing.
The head and tail functions are useful because they attempt to make the
data set readable. If you try a raw print then the output is much
less friendly.
# in this, the variable dft is a pandas data frame: dft = data frame taxis
print(dft)
pickup dropoff passengers distance fare \
0 2019-03-23 20:21:09 2019-03-23 20:27:24 1 1.60 7.0
1 2019-03-04 16:11:55 2019-03-04 16:19:00 1 0.79 5.0
2 2019-03-27 17:53:01 2019-03-27 18:00:25 1 1.37 7.5
3 2019-03-10 01:23:59 2019-03-10 01:49:51 1 7.70 27.0
4 2019-03-30 13:27:42 2019-03-30 13:37:14 3 2.16 9.0
... ... ... ... ... ...
6428 2019-03-31 09:51:53 2019-03-31 09:55:27 1 0.75 4.5
6429 2019-03-31 17:38:00 2019-03-31 18:34:23 1 18.74 58.0
6430 2019-03-23 22:55:18 2019-03-23 23:14:25 1 4.14 16.0
6431 2019-03-04 10:09:25 2019-03-04 10:14:29 1 1.12 6.0
6432 2019-03-13 19:31:22 2019-03-13 19:48:02 1 3.85 15.0
tip tolls total color payment pickup_zone \
0 2.15 0.0 12.95 yellow credit card Lenox Hill West
1 0.00 0.0 9.30 yellow cash Upper West Side South
2 2.36 0.0 14.16 yellow credit card Alphabet City
3 6.15 0.0 36.95 yellow credit card Hudson Sq
4 1.10 0.0 13.40 yellow credit card Midtown East
... ... ... ... ... ... ...
6428 1.06 0.0 6.36 green credit card East Harlem North
6429 0.00 0.0 58.80 green credit card Jamaica
6430 0.00 0.0 17.30 green cash Crown Heights North
6431 0.00 0.0 6.80 green credit card East New York
6432 3.36 0.0 20.16 green credit card Boerum Hill
dropoff_zone pickup_borough dropoff_borough
0 UN/Turtle Bay South Manhattan Manhattan
1 Upper West Side South Manhattan Manhattan
2 West Village Manhattan Manhattan
3 Yorkville West Manhattan Manhattan
4 Yorkville West Manhattan Manhattan
... ... ... ...
6428 Central Harlem North Manhattan Manhattan
6429 East Concourse/Concourse Village Queens Bronx
6430 Bushwick North Brooklyn Brooklyn
6431 East Flatbush/Remsen Village Brooklyn Brooklyn
6432 Windsor Terrace Brooklyn Brooklyn
[6433 rows x 14 columns]
# seaborn makes visualization easy - here is a scatter plot of the data.
sns.scatterplot(data=dft, x="distance", y="fare")
<AxesSubplot:xlabel='distance', ylabel='fare'>
# here's another example
sns.scatterplot(data=dft, x="pickup_borough", y="tip")
<AxesSubplot:xlabel='pickup_borough', ylabel='tip'>
# is the tip proportional to the fare?
sns.scatterplot(data=dft, x="fare", y="tip")
<AxesSubplot:xlabel='fare', ylabel='tip'>
sns.scatterplot(data=dft, x="distance", y="tip")
<AxesSubplot:xlabel='distance', ylabel='tip'>
Data as Vectors¶
Each row of the data set above gives the specific feature values for one particular observation, or measurement. This is a single data point.
We can get the names of the features using dft.columns as follows...
dft.columns
Index(['pickup', 'dropoff', 'passengers', 'distance', 'fare', 'tip', 'tolls',
'total', 'color', 'payment', 'pickup_zone', 'dropoff_zone',
'pickup_borough', 'dropoff_borough'],
dtype='object')
In this case, for each data point:
- the observation, or measurement, is a single taxi ride.
- the features of that data point are:
- 'pickup'
- 'dropoff'
- 'passengers'
- 'distance'
- 'fare'
- 'tip'
- 'tolls'
- 'total'
- 'color'
- 'payment'
- 'pickup_zone'
- 'dropoff_zone'
- 'pickup_borough'
- 'dropoff_borough'
Look again at the first six entries of the data set
dft.head(6)
| pickup | dropoff | passengers | distance | fare | tip | tolls | total | color | payment | pickup_zone | dropoff_zone | pickup_borough | dropoff_borough | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2019-03-23 20:21:09 | 2019-03-23 20:27:24 | 1 | 1.60 | 7.0 | 2.15 | 0.0 | 12.95 | yellow | credit card | Lenox Hill West | UN/Turtle Bay South | Manhattan | Manhattan |
| 1 | 2019-03-04 16:11:55 | 2019-03-04 16:19:00 | 1 | 0.79 | 5.0 | 0.00 | 0.0 | 9.30 | yellow | cash | Upper West Side South | Upper West Side South | Manhattan | Manhattan |
| 2 | 2019-03-27 17:53:01 | 2019-03-27 18:00:25 | 1 | 1.37 | 7.5 | 2.36 | 0.0 | 14.16 | yellow | credit card | Alphabet City | West Village | Manhattan | Manhattan |
| 3 | 2019-03-10 01:23:59 | 2019-03-10 01:49:51 | 1 | 7.70 | 27.0 | 6.15 | 0.0 | 36.95 | yellow | credit card | Hudson Sq | Yorkville West | Manhattan | Manhattan |
| 4 | 2019-03-30 13:27:42 | 2019-03-30 13:37:14 | 3 | 2.16 | 9.0 | 1.10 | 0.0 | 13.40 | yellow | credit card | Midtown East | Yorkville West | Manhattan | Manhattan |
| 5 | 2019-03-11 10:37:23 | 2019-03-11 10:47:31 | 1 | 0.49 | 7.5 | 2.16 | 0.0 | 12.96 | yellow | credit card | Times Sq/Theatre District | Midtown East | Manhattan | Manhattan |
The first column can be ignored - that is just a label for each observation and has nothing to do with the taxi ride data.
The pickup and dropoff columns are dates and times, we'll ignore these for now, but we will come back to them in the lab session.
The next six columns are numbers, these will fit nicely into elements one to six of a list of numbers.
We'll also ignore the remaining columns, and so we have arrived at a way of representing each data point as a vector.
Let's work through an example of how to do this.
First, note that dft.iat[0,0] will tell us what is in the first position of the
first row. Again BEWARE - indexing starts at zero. This means for example
that dft.iat[5,7] tells us what is in the eighth column of the sixth row.
An alternative to that is to use the fact that, dft.loc[5] refers to the
entire sixth row, while dft.loc[5].iat[7] refers to the eighth element in the
sixth row.
We can see all of these pieces of information with a print statement. Note
the use of \n to get new lines.
print('dft.iat[5,7] = ', dft.iat[5,7])
print('dft.loc[5].iat[7] = ', dft.loc[5].iat[7],'\n')
print('dft.loc[5] = ')
print(dft.loc[5])
dft.iat[5,7] = 12.96 dft.loc[5].iat[7] = 12.96 dft.loc[5] = pickup 2019-03-11 10:37:23 dropoff 2019-03-11 10:47:31 passengers 1 distance 0.49 fare 7.5 tip 2.16 tolls 0 total 12.96 color yellow payment credit card pickup_zone Times Sq/Theatre District dropoff_zone Midtown East pickup_borough Manhattan dropoff_borough Manhattan Name: 5, dtype: object
Let's see how we can store the numerical values for a given data point (row) in a vector. The idea is just to use an array and fill it using the methods we have just seen.
Let's remind ourself of the first few rows and store the six numerical column values (features) of the third row in a vector.
We'll need to import numpy if we haven't already.
dft.head(3)
| pickup | dropoff | passengers | distance | fare | tip | tolls | total | color | payment | pickup_zone | dropoff_zone | pickup_borough | dropoff_borough | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2019-03-23 20:21:09 | 2019-03-23 20:27:24 | 1 | 1.60 | 7.0 | 2.15 | 0.0 | 12.95 | yellow | credit card | Lenox Hill West | UN/Turtle Bay South | Manhattan | Manhattan |
| 1 | 2019-03-04 16:11:55 | 2019-03-04 16:19:00 | 1 | 0.79 | 5.0 | 0.00 | 0.0 | 9.30 | yellow | cash | Upper West Side South | Upper West Side South | Manhattan | Manhattan |
| 2 | 2019-03-27 17:53:01 | 2019-03-27 18:00:25 | 1 | 1.37 | 7.5 | 2.36 | 0.0 | 14.16 | yellow | credit card | Alphabet City | West Village | Manhattan | Manhattan |
import numpy as np
r3 = np.array([dft.iat[2,2],dft.iat[2,3],dft.iat[2,4],dft.iat[2,5],dft.iat[2,6],dft.iat[2,7]])
print(r3)
[ 1. 1.37 7.5 2.36 0. 14.16]
Too much typing? Here is a faster way...
dft.iloc[2,2:8] refers to the third row (indexed with 2), and columns $3$ to $8$
(indexed as 2 to 7).
r3 = np.array(dft.iloc[2,2:8])
print(r3)
[1 1.37 7.5 2.36 0.0 14.16]
In dft.iloc[2,2:8] the first 2 refers to the third row. The slice 2:8 uses the
starting value 2 to refer to the third column, and the colon : means continue on
from 2 in steps of 1 to get the sequence 2 3 4 \ldots. The 8 tells the
sequence to stop at 7.
If you are confused and annoyed that 2:8 gives 2 3 4 5 6 7 and not
2 3 4 5 6 7 8 then, rest assured, you are not alone.
Review¶
We have just come a long way:
- we reviewed the mathematical notion of a vector.
- we saw how using
numpyinpythonwe could- create vectors;
- add and subtract them, and multiply by a scalar;
- compute various vector norms and phoney norms.
Furthermore
- we saw how to access the toy datasets in
seaborn. - how to work with
pandasdata frames. - how to extract data frame values.
- how to represent a data point as a vector of features.
We will be building extensively on these skills in the coming weeks.
Taking raw data and manipulating it so that it is in a form suitable
for analysis is often referred to as Data Wrangling. The pandas
cheat sheet here https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf
gives lots of examples of how to work with data frames.
For now we finish off with a look at a few more of the toy datasets
that seaborn provides. They are called toy because they are
realistic enough to use when learning techniques and tools in
data science, but also small enough to get answers in real time.
The tips data set¶
Let's look again now at the tips data set.
We will load the data using the variable name dftp, for data frame tips.
Note that we could use dft, the same name as above, but that would overwrite
the previous 'value/meaning' of dft. This may or may not be what you want.
dftp = sns.load_dataset('tips')
dftp.head()
| total_bill | tip | sex | smoker | day | time | size | |
|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 1.01 | Female | No | Sun | Dinner | 2 |
| 1 | 10.34 | 1.66 | Male | No | Sun | Dinner | 3 |
| 2 | 21.01 | 3.50 | Male | No | Sun | Dinner | 3 |
| 3 | 23.68 | 3.31 | Male | No | Sun | Dinner | 2 |
| 4 | 24.59 | 3.61 | Female | No | Sun | Dinner | 4 |
An extensive list of data frame methods/functions can be found here: https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.html#pandas.DataFrame - we have seen some of them. Let's look at some more...
This will give us basic information on the data set.
print(dftp.info)
<bound method DataFrame.info of total_bill tip sex smoker day time size 0 16.99 1.01 Female No Sun Dinner 2 1 10.34 1.66 Male No Sun Dinner 3 2 21.01 3.50 Male No Sun Dinner 3 3 23.68 3.31 Male No Sun Dinner 2 4 24.59 3.61 Female No Sun Dinner 4 .. ... ... ... ... ... ... ... 239 29.03 5.92 Male No Sat Dinner 3 240 27.18 2.00 Female Yes Sat Dinner 2 241 22.67 2.00 Male Yes Sat Dinner 2 242 17.82 1.75 Male No Sat Dinner 2 243 18.78 3.00 Female No Thur Dinner 2 [244 rows x 7 columns]>
A quick glance tell us that there are $7$ columns of features, and $244$ data points.
We can these numbers with shape, and size tells us how many distinct
values are stored.
print('The shape of the data frame is: ', dftp.shape)
print('The size of the data frame is: ', dftp.size)
print('Note that 244*7 =', 244*7)
The shape of the data frame is: (244, 7) The size of the data frame is: 1708 Note that 244*7 = 1708
One way to get a quick overview of the data is to plot the numerical values.
dftp.plot()
<AxesSubplot:>
We can get summary statistics like this:
dftp.describe()
| total_bill | tip | size | |
|---|---|---|---|
| count | 244.000000 | 244.000000 | 244.000000 |
| mean | 19.785943 | 2.998279 | 2.569672 |
| std | 8.902412 | 1.383638 | 0.951100 |
| min | 3.070000 | 1.000000 | 1.000000 |
| 25% | 13.347500 | 2.000000 | 2.000000 |
| 50% | 17.795000 | 2.900000 | 2.000000 |
| 75% | 24.127500 | 3.562500 | 3.000000 |
| max | 50.810000 | 10.000000 | 6.000000 |
And we can get more detailed quantile information like this
dftp.quantile(q = 0.95, numeric_only=True) # OK in binder, Jan 2025.
#dftp.quantile(0.95) # this didn't work in binder as of jan 2024.
total_bill 38.0610 tip 5.1955 size 4.0000 Name: 0.95, dtype: float64
# alternatives - with thanks to Kevon Brown (MSc student 2023-24)
print(dftp['total_bill'].quantile(0.95))
print(dftp['tip'].quantile(0.95))
print(dftp['size'].quantile(0.95))
38.061 5.1955 4.0
We can also produce scatter plots
sns.scatterplot(data=dftp, x="total_bill", y="tip")
<AxesSubplot:xlabel='total_bill', ylabel='tip'>
Exercises¶
For the Anscombe data set:
- Which of the summary statistics for $x$ are the same or similar for each subset?
- Which of the summary statistics for $y$ are the same or similar for each subset?
Look at the diamonds data set
- How many diamonds are listed there? How many attributes does each have?
- Scatter plot price against carat.
1: ds = sns.load_dataset('diamonds'); ds.shape: 53940 and 10
2: sns.scatterplot(data=ds, x="carat", y="price")